Tingkat lanjut dari pembahasan tentang gerak adalah gerak dalam ruang dua dimensi. Gerak ini dapat berupa gerak parabola (gerak peluru), gerak melingkar, gerak dalam lintasan elips, dan hiperbola. Namun dalam artikel ini kita hanya akan membahas tentang gerak parabola (gerak peluru).
Pada gerak dua dimensi, posisi benda akan secara lengkap terdefinisikan apabila kita menggunakan dua buah koordinat posisi, yaitu koordinat x dan y yang saling tegak lurus. Untuk menentukan arah sumbu x dan y kita dapat memilihnya secara acak asal tegak lurus. Pemilihan arah dilakukan untuk mempermudah menyelesaikan persoalan. Contohnya pada gerak sepanjang bidang miring kita sering memilih arah sumbu x searah kemiringan bidang dan sumbu y tegak lurus bidang. Pada persoalan lain sumbu x sering dipilih berarah horisontal sedangkan sumnbu y berarah vertikal ke atas.
Gerak Parabola (Gerak Peluru)
Salah satu gerak dua dimensi yang paling popular adalah gerak parabola atau gerak parabola, dan dalam artikel ini kita akan menggunakan istilah gerak peluru. Disebut gerak peluru karena gerak ini yang akan dilalui atau ditempuh oleh peluru yang ditembakkan ke atas yang membentuk sudut tertentu terhadap arah horizontal (tidak vertikal ke atas) atau yang ditembakkan dengan sudut sembarang dari ketinggian tertentu. Namun gerak ini bukan hanya diterapkan untuk mebahas peluru. Setiap benda yang dilempat ke atas dalam arah tidak vertikal atau ditembakkan dengan sudut sembarang dari ketinggian tertentu melakukan gerak peluru.
Sekarang kita mulai membahas gerak peluru secara detail. Pada saat ditembakkan, peluru memiliki dua komponen kecepatan. Komponen kecepatan arah horisontal dan arah vertikal adalah

;
)
Peluru yang ditembakkan dengan kecepatan awal membentuk sudut elevasi tertentu terhadap sumbu datar akan mengambil lintasan seperti pada Gambar 1.
 Gambar 1. Bentuk umum lintasan peluru
Gambar 1. Bentuk umum lintasan peluru Akibat adanya percepatan gravitasi bumi, lintasan gerak peluru akan selalu melengkung ke bawah. Untuk komponen kecepatan dalam arah horizontal akan selalu tetap selama peluru bergerak, yang berubah-ubah adalah komponen arah vertical. Perbedaan ini diakibatkan karena dalam arah vertikal ada percepatan gravitasi yang berarah ke bawah sedangkan dalam arah horizontal tidak ada percepatan seperti yang ditunjukkan pada gambar 2. Mula-mula makin kecil dan saat di puncak lintasan, komponen kecepatan arah vertical nol. Kemudian komponen kecepatan membesar kembali namun arahnya berlawanan (arah ke bawah).
 Gambar 2. Peluru mendapat percepatan ke bawah (gravitasi) dan tidak mendapat percepatan arah horizontal.
Gambar 2. Peluru mendapat percepatan ke bawah (gravitasi) dan tidak mendapat percepatan arah horizontal.Jika kita ambil arah ke kanan sejajar dengan sumbu x positif dan arah ke atas sejajar dengan sumbu y positif maka komponen kecepatan gerak

;
)
Dengan demikian, kecepatan gerak peluru tiap saat adalah
...(3))
sedangkan untuk posisi peluru tiap saat adalah
=r_{0}+\int_{0}^{t}vdt=r_{0}+\int_{0}^{t}(v_{0}cos\theta&space;+(v_{0}sin\theta&space;-gt)))
=r_{0}+v_{0}tcos\theta&space;t+((v_{0}tsin\theta&space;-\frac{1}{2}gt^{2}))...(4))
dengan r0 adalah posisi peluru pada saat t = 0.
Dari persamaan komponen kecepatan maka kita dapat menentukan sudut yang dibentuk oleh vektor kecepatan terhadap arah horisontal. Misalkan sudut tersebut adalah φ (Gambar 3) maka


)
Dari persamaan (5) kita dapatkan sejumlah informasi. Pada puncak lintasan peluru hanya memiliki kecepatan arah horizontal. Dengan demikian pada puncak lintasan berlaku φ = 0 atau tan φ = 0. Misalkan waktu yang diperlukan sejak peluru ditembakkan hingga mencapai puncak lintasan adalah tm maka berlaku

yang menghasilkan
)
Kapan peluru mencapai tanah kembali? Kita asumsikan bahwa ketinggian tempat penembakan sama dengan ketinggian tempat jatuh peluru. Pada saat penembakan, t = 0, terpenuhi φ=θ dimana

Dengan memperhatikan Gambar 3 jelas bahwa pada saat peluru kembali menyentuh tanah maka sudut yang dibentuk oleh vector kecepatan memenuhi φ = -θ. Jika saat ini waktu tempuh adalah T maka persamaan (5) dapat ditulis
 Gambar 3
Gambar 3
atau
)
Dari persamaan ini tampak bahwa T = 2tm atau waktu yang diperlukan untuk mencapai tanah kembali sama dengan dua kali waktu untuk mencapai puncak lintsan.
Gambar 4 memperlihatkan posisi maksimum yang dicapai peluru dan jangkauan peluru.
 Gambar 4
Gambar 4Berapakan nilai-nilai tersebut? Mari kita coba hitung. Dengan menggunakan persamaan (4) kita dapat menentukan posisi peluru pada saat tm, yaitu
=r_{0}+v_{0}t_{m}cos\theta+((v_{0}t_{m}sin\theta&space;-\frac{1}{2}gt_{m}^{2})))
Substitusi tm dari persamaan (6) sehingga diperoleh
=r_{0}+v_{0}cos\theta&space;(\frac{v_{0}}{g}sin\theta)+((v_{0}(\frac{v_{0}}{g}sin\theta)sin\theta&space;-\frac{1}{2}g(\frac{v_{0}}{g}sin\theta)^{2})))
=r_{0}+\frac{v_{0}^{2}}{g}sin\theta&space;cos\theta&space;+\frac{v_{0}^{2}}{2g}sin^{2}\theta&space;...(8))
Dari persamaan (8) kita simpulkan bahwa ketinggian maksimum yang dicapai peluru adalah
)
Jarak dalam arah x tepat di bawah puncak lintasan adalah
)
di mana kita telah menggunakan hubungan trigonomentri sin 2θ= 2sin θ cos θ.
Dengan menggunakan T pada persamaan (7) maka posisi peluru saat kembali mencapai tanah adalah
=r_{0}+v_{0}Tcos\theta+((v_{0}Tsin\theta-\frac{1}{2}gT^{2})))
=r_{0}+v_{0}(&space;\frac{2v_{0}}{g}sin\theta&space;)cos\theta+((v_{0}(&space;\frac{2v_{0}}{g}sin\theta&space;)sin\theta-\frac{1}{2}g(&space;\frac{2v_{0}}{g}sin\theta&space;)^{2})))
=r_{0}+\frac{2&space;v_{0}^{2}&space;sin\theta&space;cos\theta&space;}{g}...(11))
Kita definisikan jarak tempuh sebagai jarak horizontal dari titik penembakan benda ke titik jatuh peluru di tanah (asumsi titik penembakan dan titik jatuh berada pada bidang datar). Dengan mengacu pada persamaan (11) maka jarak tempuh adalah
)
Pertanyaan menarik adalah berapakah sudut penembakan agar dicapai jarak tempuh maksimum? Mengingat nilai maksimum sin 2θ = 1 maka jarak tempuh maksimum akan dicapai jika sin 2θ=1. Sudut yang nilai sinusnya satu adalah 90o. Dengan demikian sudut penembakan yang menghasilkan jangkauan maksimum memenuhi 2θ= 90o atau θ=45o . Dengan sudut ini maka jangkauan maksimum adalah
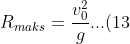)
Contoh Soal
Dari lereng sebuah bukit pada ketinggian 16 meter dilemparkan sebuah batu dengan kecepatan 5m/s bersudut arah 37o terhadap arah mendatar. jika percepatan gravitasi 10m/s2 tentukanlah: kedudukan batu saat mencapai titik tertinggi
Untuk mengetahui kedudukan batu saat mencapai titik tertinggi, kita memasukkan variabel yang di ketahui ke dalam persamaan 9 untuk komponen sumbu y, dan persamaan 10 untuk komponen sumbu x.
=&space;1,2)
^{2}=&space;16,45)
Hikmah
Membahas tentang gerak banyak pelajaran yang bisa kita ambil dari satu di antara sekian banyaknya materi dalam ilmu fisika. Terkhusus bagi kita sebagai penuntu ilmu. Dalam syairnya Imam Asy-Syafi’i berkata:
Berdiam diri, stagnan, dan menetap di tempat mukm, sejatinya bukanlah peristirahatan bagi mereka pemilik akal dan adab, maka berkelanalah, tinggalkan negerimu (demi menuntut ilmu dan kemuliaan)
Safarlah, engkau akan menemukan pengganti orang-orang yang engkau tinggalkan. Berpeluhlah engkau dalam usaha dan upaya, karena lezatnya kehidupan baru terasa setelah engkau merasakan payah dan peluh dalam bekerja dan berusaha.
Sungguh aku melihat, air yang tergenang dalam diamnya, justru akan tercemar lalu membusuk. Jika saja air tersebut mengalir, tentu ia akan terasa lezat menyegarkan. Tidak demikian jika ia tidak bergerak mengalir.
Sekawanan singa, andai tidak meninggalkan sarangya, niscanya kebuasannya tidak lagi terasah, ia pun akan mati karena lapar. Anak panah, andai tidak melesat meninggalkan busurnya, maka jangan pernah bermimpi akan mengenai sasaran.
Sang surya, andai selalu terpaku di ufuk, niscaya ia akan dicela oleh segenap ras manusia, dari ras Arabia, tidak terkecuali selain mereka.
Dan bijih emas yang masih terkubur dibebatuan, hanyalan sebongkah batu tak berharga, yang terbengkalai di tempat asalnya. Demikian halnya dengan gaharu di belantara hutan, hanya sebatang kayu, sama seperti kayu biasa lainnya.
Andai saja gaharu tersebut keluar dari belantara hutan, ia adalah parfum yang bernilai tinggi. Dan andaikan bijih itu keluar dari tempatnya, ia akan menjadi emas yang berharga.