Kinematika bagian kedua kali ini kita akan membahas tentang gerak lurus berubah beraturan (GLBB). Jika percepatan partikel bervariasi dalam waktu, gerakannya bisa rumit dan sulit untuk menganalisa. Namun, kinematika jenis gerakan satu dimensi yang sangat umum dan sederhana adalah bahwa percepatannya konstan atau biasa kita sebut GLBB.
Kita mulai dengan rumus percepataan rata-rata
Dikarenakan ti=0 dan tf=t, dapat diperoleh
atau
Persamaan di atas memungkinkan kita untuk menentukan kecepatan suatu objek setiap saat t jika kita mengetahui kecepatan awal objek vi dan percepatan a yang konstan
Karena kecepatan pada percepatan konstan bervariasi secara linier dalam waktu sesuai dengan Persamaan 2, kita dapat mendefinisikan kecepatan rata-rata dalam setiap interval waktu sebagai rata-rata dari kecepatan awal dan kecepatan akhir:
Perhatikan bahwa persamaan untuk kecepatan rata-rata ini hanya berlaku dalam situasi di mana percepatan konstan. untuk mendapatkan posisi objek sebagai fungsi waktu; kita kembali pada persamaan kecepatan rata-rata dimana ∆x=xf - xi, dan ∆t=tf-ti =t-0. sehingga
atau
Kita dapat memperoleh persamaan lain yang bermanfaat untuk posisi partikel di bawah percepatan konstan; dengan mensubtitusi Persamaan 2 ke Persamaan 4:
atau
kita juga dapat memperoleh persamaan untuk kecepatan akhir yang tidak mengandung waktu sebagai variabel; dengan mensubstitusi nilai t dari Persamaan 2 ke dalam Persamaan 4:
diperoleh
Sebuah partikel di bawah percepatan konstan bergerak sepanjang sumbu x: (a) grafik posisi– waktu, (b) grafik kecepatan-waktu, dan (c) grafik percepatan-waktu Degan metode integral
- kita mulai dari definisi percepatan sesaat,
Kemudian kita integralkan kedua ruas dengan batas kecepatan dari Vo ke V; dan batas waktu dari to ke t.

Diperoleh

Atau

Selanjutnya kita integralkan untuk waktu, diperoleh

- Kita berangkat dari definisi kecepatan sesaat

Kemudian kita integralkan kedua ruas dengan batas posisi dari ro ke r; dan batas waktu dari to ke t.

Diperoleh

Kasus khusus untuk gerak dengan percepatan yang konstan

Karena v=dx/dt, percepatan juga dapat ditulis sebagai
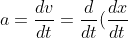=\frac{d^{2}x}{d^{2}t})
sumber pustaka